Input Files
Introduction
An explicit stamping simulation is followed by a spring-back analysis using implicit or explicit solvers for stress relaxation.
| Note |
|---|
NOTE: Currently (September 2022) the Implicit solution sequence is not yet available in OpenRadioss so only the Explicit springback solution will work. |
The spring-back simulation of sheet metal bent into a hat-shape is studied. The problem is one of the famous tests from the Numisheet'93. As spring-back is generally a quasi-static unloading, the use of the OpenRadioss implicit solver is justified. The OpenRadioss explicit solver is also used to compare the method's efficiency. However, for the stamping phase only the explicit solver is used, as the forming process is highly dynamic.
The example illustrates how to link up the explicit computations. It highlights the efficiency of the implicit solver for the spring-back simulation.
Options and Keywords Used
Keyword documentation may be found in the reference guide available from
...
Explicit stamping simulation, implicit / explicit spring-back simulation, and stress relaxation
Implicit strategy and time step control by arc-length method
Anisotropic elasto-plastic material law (/MAT/LAW43 (HILL_TAB)) and Hill model
Orthotropic shell formulation, QEPH, progressive plastification, and iterative plasticity
Interface (/INTER/TYPE7), Penalty method, and friction
Concentrated load (/CLOAD)
Dynamic relaxation (/DYREL)
Implicit parameters (Implicit Solution)
Implicit spring-back (/IMPL/SPRBACK)
Imposed velocity (/IMPVEL)
Rigid body (/RBODY)
Model Description
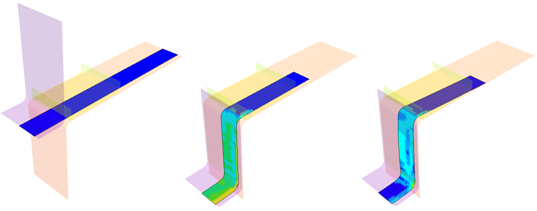
This example deals with the numerical simulation of a stamping process, including the spring-back.
...
The yield curve used is shown in Figure 3. Failure is not taken into account.
...
Simulation Iterations
Taking symmetry into account, only a quarter of the structure is modeled. The symmetry plane is along axis y = 17.5 mm and x = 0 mm.
...
| Linear Solver Method N=2 Direct solver MUMPS Precondition Methods Icpre=5 Factored approximate inverse Maximum Iterations Number It_max=0 System dimension (NDOF) Stop Criteria Itol=0 Relative residual on matrix Tolerance for Stop Criteria Tol=0 Machine precision |
Refer to OpenRadioss Starter Input for more details about implicit options.
...
If the /ADYREL keyword is used, no parameter is required to be input, since OpenRadioss automatically computes them.
Results
In the metal stamping operation, the highly nonlinear deformation processes tend to generate a large amount of elastic strain energy in the metal material in addition to some of the plastic deformed areas. The internal energy, which is stored in the sheet metal during stamping, is subsequently released once the stamping pressure has been removed. This energy released is the driving force of the spring-back in the sheet metal forming process. Therefore, the spring-back deformation for sheet metal forming is mainly due to the amount of elastic energy stored in the part while it is being plastically deformed.
...